Siv's Blog - Graph embeddings

Fonte -> https://iamsiva11.github.io/graph-embeddings-2017-part1/

Fonte -> https://iamsiva11.github.io/graph-embeddings-2017-part2/

Network Representation Learning (aka. graph embeddings)

2017: state of art graph embedding techniques (approaches like random walk based , deep learning based, etc)

decomposed machine learning into three components: (1) Representation, (2) Evaluation, and (3) Optimization

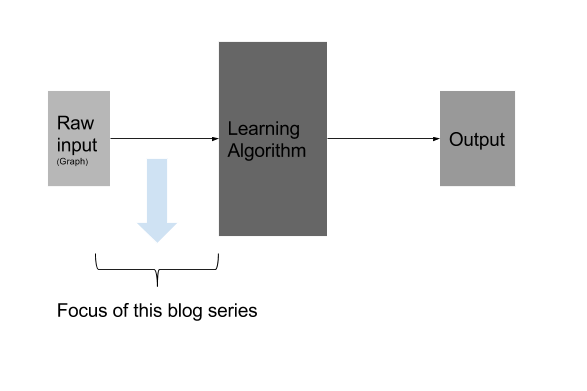
Representation is basically representing the input data (be image, speech, or video for that matter) in a way the learning algorithm can easily process. Representation Learning is using learning algorithms to derive good features or representation automatically, instead of traditional hand-engineered features. 

representation learning (aka. feature engineering/learning)

deep learning ... Multilayer neural networks can be used to perform feature learning, since they learn a representation of increasing complexity/abstraction of their input at the hidden layer(s) which is subsequently used for classification or regression at the output layer.

So basically, we have two learning tasks now. First, we let the deep network discover the features and next place our preferred learning model to perform your task. Simple!

one-hot encoding, Bag of words, N-gram, TF-IDF: don’t have any notion of either syntactic or semantic similarity between parts of language.

 

Representation of words as vectors (aka. embedding) Word2Vec or GloVE

When applying deep learning to natural language processing (NLP) tasks, the model must simultaneously learn several language concepts: the meanings of words, how words are combined to form concepts (i.e., syntax), how concepts relate to the task at hand.

Mathematically, embedding maps information entities into a dense, real-valued, and low-dimensional vectors.

Specifically, in a multitude of different fields, such as: Biology, Physics, Network Science, Recommender Systems and Computer Graphics; one may have to deal with data defined on non-Euclidean domains (i.e. graphs and manifolds)

Graphs are a ubiquitous data structure. Social networks, molecular graph structures, biological protein-protein networks, recommender systems—all of these domains and many more can be readily modeled as graphs, which capture interactions (i.e., edges) between individual units (i.e., nodes). As a consequence of their ubiquity, graphs are the backbone of countless systems, allowing relational knowledge about interacting entities to be efficiently stored and accessed. However, graphs are not only useful as structured knowledge repositories: they also play a key role in modern machine learning. The central problem in machine learning on graphs is finding a way to incorporate information about the structure of the graph into learning algorithms.

Generally, graph embedding aims to represent a graph as low dimensional vectors while the graph structure are preserved. We may represent a node or edge or path or substructure or whole-graph (at different levels of granularity) as a low-dimensional vector.

The differences between different graph embedding algorithms lie in how they define the graph property to be preserved.

Graph representation learning does not require the learned representations to be low dimensional.

graph embeddings converts the graph data into a low dimensional space in which the graph structural information and graph properties are maximally preserved.

There are different types of graphs (e.g., homogeneous graph, heterogeneous graph, attribute graph, graph with auxiliary information, graph constructed from non-relational data, etc), so the input of graph embedding varies in different scenarios. 

Different types of embedding input carry different information to be preserved in the embedded space and thus pose different challenges to the problem of graph embedding. For example, when embedding a graph with structural information only, the connections between nodes are the target to preserve.

The most common type of embedding output is node embedding which represents close nodes as similar vectors. Node embedding can benefit the node related tasks such as node classification, node clustering, etc. 

However, in some cases, the tasks may be related to higher granularity of a graph e.g., node pairs, subgraph, whole graph. Hence the first challenge in terms of embedding output is how to find a suitable embedding output type for the specific application task.

Furthermore, Choice of property, Scalability, Dimensionality of the embedding are other few challenges that has to be addressed.

1. Choice of property : A “good” vector representation of nodes should preserve the structure of the graph and the connection between individual nodes. The first challenge is choosing the property of the graph which the embedding should preserve. Given the plethora of distance metrics and properties defined for graphs, this choice can be difficult and the performance may depend on the application.

2. Scalability : Most real networks are large and contain millions of nodes and edges — embedding methods should be scalable and able to process large graphs. Defining a scalable model can be challenging especially when the model is aimed to preserve global properties of the network.

3. Dimensionality of the embedding: Finding the optimal dimensions of the representation can be hard. For example, higher number of dimensions may increase the reconstruction precision but will have high time and space complexity. The choice can also be application-specific depending on the approach: E.g., lower number of dimensions may result in better link prediction accuracy if the chosen model only captures local connections between nodes.

The applications fall under three of three following categories: node related, edge related and graph related.

• Node Related Applications - Node Classification and semi-supervised learning, Clustering, Node Recommendation/Retrieval/Ranking, Clustering and community detection.
• Edge Related Applications - Link Prediction and Graph Reconstruction.
• Graph Related Application - Graph Classification, Visualization and pattern discovery, Network compression.

In the early 2000s, researchers developed graph embedding algorithms as part of dimensionality reduction techniques.

Since 2010, research on graph embedding has shifted to obtaining scalable graph embedding techniques which leverage the sparsity of real-world networks.

Recently (2017), on of the pioneering algorithm in graph embedding technique was “DeepWalk” [8],... And more importantly, of these methods general non-linear models(e.g. deep learning based) have shown great promise in capturing the inherent dynamics of the graph.

Matrix factorisation based graph embedding represent graph property (e.g., node pairwise similarity) in the form of a matrix and factorize this matrix to obtain node embedding. The problem of graph embedding can thus be treated as a structure-preserving dimension reduction method which assumes the input data lie in a low dimensional manifold.  

Random walks have been used to approximate many properties in the graph including node centrality and similarity. They are especially useful when one can either only partially observe the graph, or the graph is too large to measure in its entirety: DeepWalk and node2vec are two examples

The growing research on deep learning has led to a deluge of deep neural networks based methods applied to graphs. Deep auto-encoders have been e.g. used for dimensionality reduction due to their ability to model non-linear structure in the data. 

As a popular deep learning model, Convolutional Neural Network (CNN) and its variants have been widely adopted in graph embedding. Recent one being, Graph Convolutional Networks(GCN)[9] [ICLR 2017].